Understanding Arrhenius for Reliability

Reliability engineering is all about predicting how long a product will last under specific conditions. One of the most fundamental tools for this prediction is the Arrhenius equation, which models the effect of temperature on reaction rates—and by extension, on failure mechanisms in materials and systems.

The Arrhenius Equation: A Foundation of Reliability Modeling

The Arrhenius equation mathematically relates the rate of a chemical reaction (or failure process) to temperature:

t_f = A \cdot e^{-\frac{E_a}{kT}}

Where:

t_f: Time to failure
A: Pre-exponential factor (a constant for the material or process)
E_a: Activation energy (the energy barrier for the reaction)
k: Boltzmann constant (8.617 × 10⁻⁵ eV/K)
T: Absolute temperature in Kelvin

This equation shows that as temperature increases, time to failure decreases exponentially—a critical insight for accelerated testing.

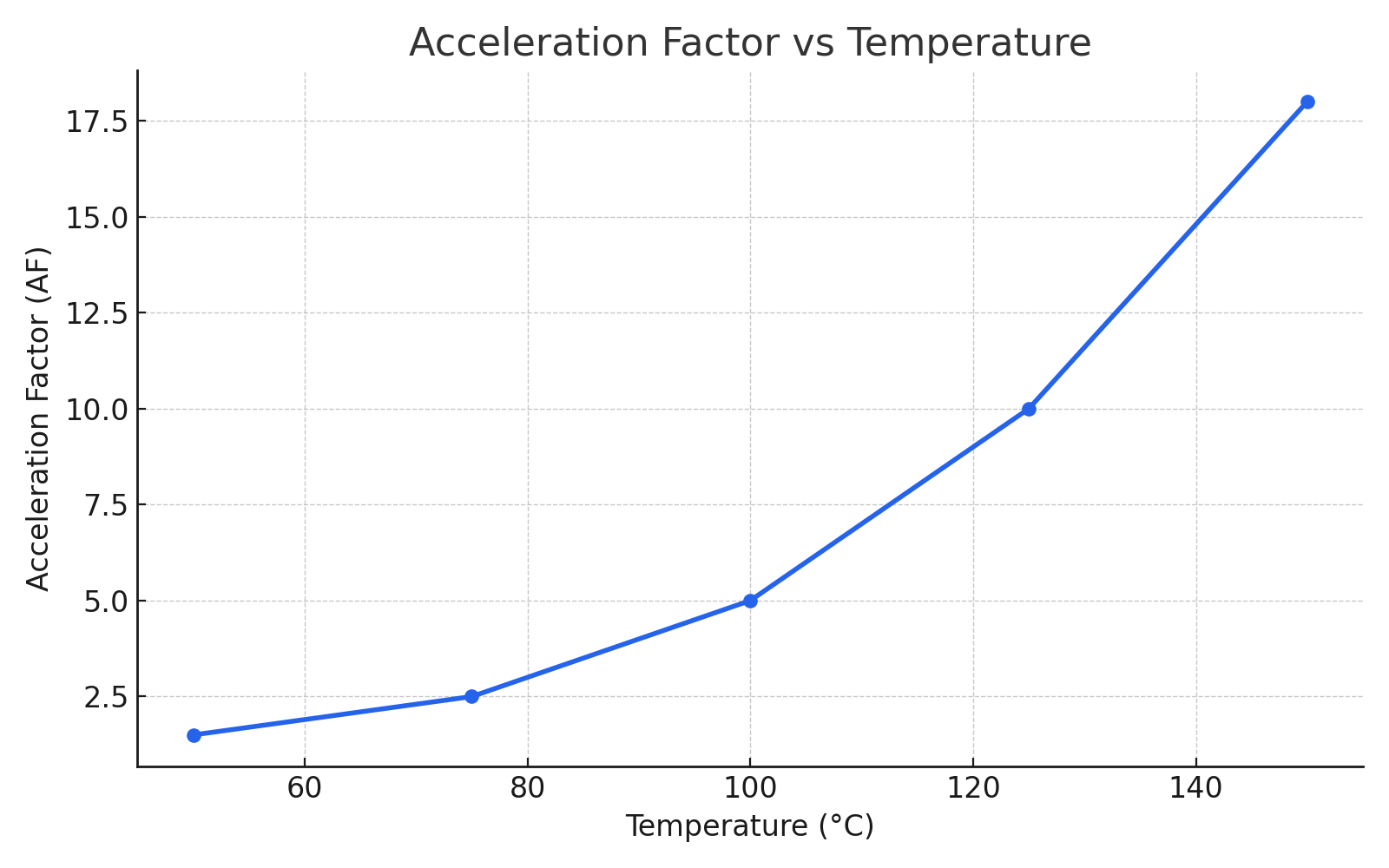
Graph: Acceleration Factor vs. Temperature

The graph below illustrates how the acceleration factor increases with temperature for a typical activation energy:

Why Activation Energy Matters

Activation energy $E_a$ represents the minimum energy required for a reaction to occur. In reliability, this translates to the energy needed for a failure mechanism (e.g., electromigration, thermal breakdown) to manifest.

Different materials and failure modes have different $E_a$ values:

For metals in microelectronics (e.g., aluminum, copper), $E_a$ typically ranges from 0.5 to 1.0 eV.
For polymers in automotive components, values can vary widely based on additives, fillers, and degradation modes (thermal oxidation, hydrolysis).

Acceleration Factor: Predicting Life from Tests

One of the most powerful uses of Arrhenius is calculating the Acceleration Factor (AF)—how much faster a failure occurs at an elevated test temperature compared to normal use:

AF = \exp \left( \frac{E_a}{k} \left( \frac{1}{T_{use}} - \frac{1}{T_{test}} \right) \right)

For example, an automotive control module might undergo a 1000-hour test at 125°C. Using Arrhenius, engineers can estimate that this is equivalent to 10 years at 55°C in the field. This capability is essential for industries like:

Automotive: Validating ECUs, sensors, and connectors to withstand years of harsh thermal exposure.
Microelectronics: Testing chips and packages under accelerated thermal and voltage stresses to predict long-term reliability.

Real-World Applications

Automotive Industry: Simulating a Decade in Weeks

In the Robustness Validation process for automotive electronic modules, the Arrhenius model underpins burn-in tests and mission profile validations. By applying realistic environmental stressors (e.g., -40°C to +125°C temperature ranges, vibration, humidity), engineers ensure that control units, sensors, and actuators can survive 15 years of vehicle life. The ZVEI Handbook provides structured methodologies for integrating Arrhenius-based models into testing protocols.

Curious how temperature affects your reliability? Check out our Arrhenius Calculator for quick estimates.

Microelectronics: Managing Thermal Risks

In microelectronics, the Arrhenius equation helps predict failure mechanisms like electromigration and dielectric breakdown. For example, a chip operating at 85°C may fail in 10 years, but testing at 150°C can simulate this lifetime in just a few months. The NASA Physics of Failure Handbook emphasizes the importance of understanding the underlying failure physics—not just applying the equation blindly.

Want to estimate your own short burn-in test conditions to check for early failures? Try our Burn-In Wizard to simulate equivalent field life from accelerated test plans.

Limitations and Cautions

Not all failures are thermally activated: Mechanical fatigue, corrosion, and radiation may require different models.
Test temperatures must be realistic: Exceeding material limits can introduce failure mechanisms (e.g., melting solder, dielectric breakdown) that wouldn't occur in the field.
Assumptions of constant $E_a$ : May not hold across different materials, temperatures, or combined stresses (e.g., temperature and humidity in the Peck model).

Conclusion: A Tool, Not a Crystal Ball

The Arrhenius equation remains a cornerstone of accelerated life testing and physics-of-failure reliability engineering. By understanding the materials, the failure modes, and the operating environment, engineers can use Arrhenius-based models to predict, validate, and improve product reliability—whether it’s a car’s control module surviving 15 years on the road or a microchip enduring a decade of power cycling.

Ready to try it yourself? Visit our Arrhenius Calculator and Burn-In Wizard to simplify your reliability test planning today.